Web Appendix for numerical language comparison 2018

Web appendix for numerical language comparison (2018)

We compare four numerical languages in a Vox blog post.

Section 3 of the blog post compares running times for the calculation of GARCH log-likelihood. It is a good representative example of the type of numerical problem we often encounter. Because the values at any given time t depend on values at t-1, this loop is not vectorisable. The GARCH(1,1) specification is

$$\sigma_t^2= \omega + \alpha y^2_{t-1}+ \beta \sigma_{t-1}^2$$

with its log-likelihood given by

$$\ell=-\frac{T-1}{2} \log(2\pi)-\frac{1}{2}\sum_{t=2}^T \left[ \log \left(\omega+\alpha y_{t-1}^2+\beta\sigma_{t-1}^2\right)+\frac{y_t^2}{\omega+\alpha y_{t-1}^2+\beta\sigma_{t-1}^2} \right]$$

For the purposes of our comparison, we are only concerned with the iterative calculation involved for the second term. Hence, the constant term on the left is ignored.

We coded up the log-likelihood calculation in the four languages and in C, keeping the code as similar as possible between languages. We then simulated a sample of size 10,000, loaded that in, and timed the calculation of the log-likelihood 1000 times (wall time), picking the lowest in each case.

The code can be downloaded here.

C

The fastest calculation is likely to be in C (or FORTRAN)

gcc -march=native -ffast-math -Ofast run.c
double likelihood(double o, double a, double b, double h, double y2, int N){	
	double lik=0;
	for (int j=1;j<N;j++){
		h = o+a*y2[j-1]+b*h;	
		lik += log(h)+y2[j]/h;
	}
	return(lik);   
}

R

R does not really have a good just-in-time (JIT) compiler so it is likely slow.

likelihood =function(o,a,b,y2,h,N){
	lik=0
	for(i in 2:N){
		h=o+a*y2[i-1]+b*h
		lik=lik+log(h)+y2[i]/h
	}
	return(lik)	
}

Python

Python is likely to be quite slow,

def likelihood(hh,o,a,b,y2,N):
    lik = 0.0
    h = hh
    for i in range(1,N):
        h=o+a*y2[i-1]+b*h
        lik += np.log(h) + y2[i]/h
    return(lik)

but will be significantly sped up by using Numba.

from numba import jit
@jit
def likelihood(hh,o,a,b,y2,N):
    lik = 0.0
    h = hh
    for i in range(1,N):
        h=o+a*y2[i-1]+b*h
        lik += np.log(h) + y2[i]/h
    return(lik)

MATLAB/Octave

(Octave's syntax was designed to be largely compatible with MATLAB, as an open-source alternative)

function lik = likelihood(o,a,b,h,y2,N)
    lik=0;
    for i = 2:N
        h=o+a*y2(i-1)+b*h;
        lik=lik+log(h)+y2(i)/h;
    end
end

Julia

function likelihood(o,a,b,h,y2,N)
    local lik=0.0
    for i in 2:N
        h = o+a*y2[i-1]+b*h
        lik += log(h)+y2[i]/h
    end
    return(lik)
end

Results

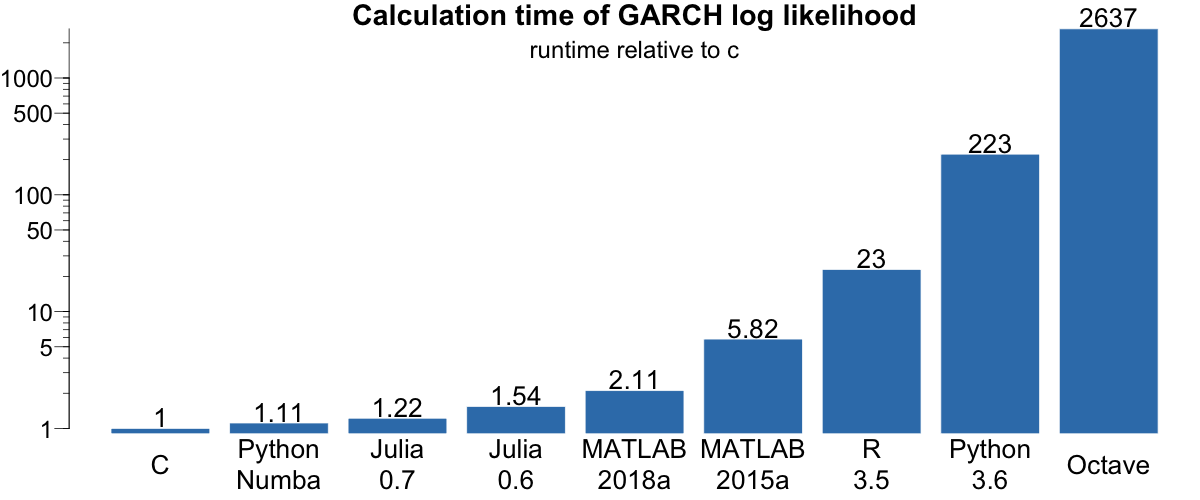
We tried two versions of Matlab (2015a, 2018a), Octave 4.4, R 3.5, Python 3.6 and two versions of Julia (0.6 and 0.7). All runtime results are presented relative to the fastest (C). All code ran on a late model iMac.

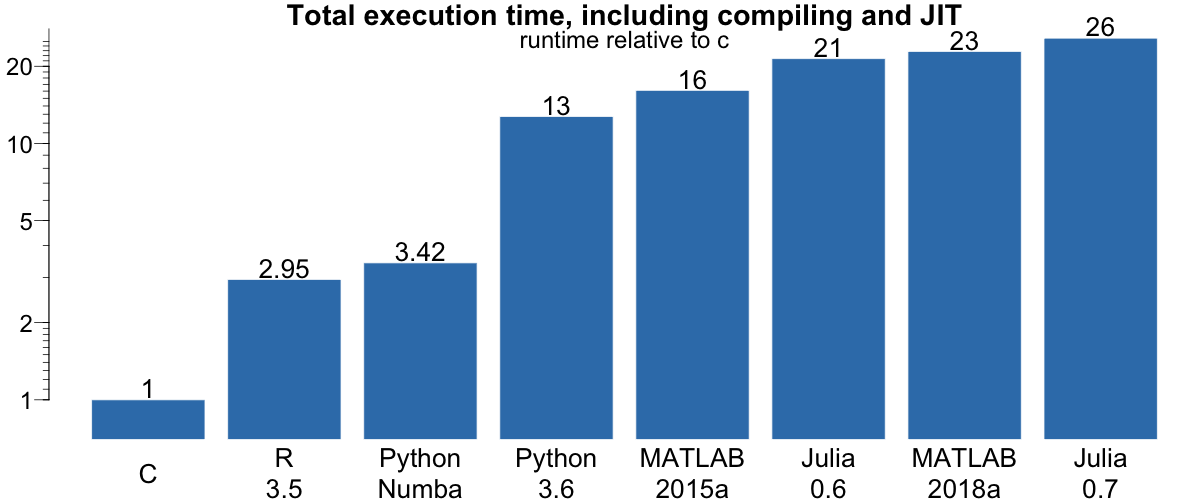
In a practical implementation, the log-likelihood calculation is only a part of the total time. We also timed the total execution time, including the starting and stopping of the software package, and compile time in the case of C. This was done in the terminal with a command like

time python run.py

C, even when including the compile time remains fastest, but now followed by R.

Conclusion

Generally, languages having poorer just-in-time compiling performed worse. However, there exist many tricks that can shorten processing time significantly. For instance, Python's Numba package allows for efficient just-in-time compiling with minimal additional code — implementing Numba led to the calculation here being 200 times faster. Cython is also possible, but it is much more involved than Numba. For all the languages, embedding C code for the loop is possible, and would lead to performance improvements.

Julia's performance is impressive, reflecting its advantage due to features like just-in-time compiling. Moreover, the difference between 0.6 and 0.7 reflects the progress made in the language's development.

The results for Octave and MATLAB 2015a/2018a are reflective of the improvements MATLAB has made in terms of speeding up its code processing, in particular the introduction of JIT compiling in MATLAB's execution engine from MATLAB 2015b onward.

One can of course bypass many of those issues by just coding up the GARCH likelihood in C, including the optimisation, and calling that within any of the languages. This is indeed what we do in our own work via Rccp.